Representing hierarchical data can be a challenging task in relational databases. Tree structures in SQL are a fundamental solution to this problem, allowing you to organize data hierarchically, just like the branches of a tree. In this blog post, let’s dive into the world of tree structures in SQL with zen8labs, exploring the advantages, disadvantages, and providing practical examples to help you understand when and how to use tree structures effectively.
Basic concepts
- Nodes: each element in a tree structure is called a node.
- Root nodes: this is the starting point of a tree
- Parent and child nodes: nodes can have “parent” and “child” relationships.
- Leaf: nodes that have no child are called “leaf nodes”. They are endpoints of the tree branches.
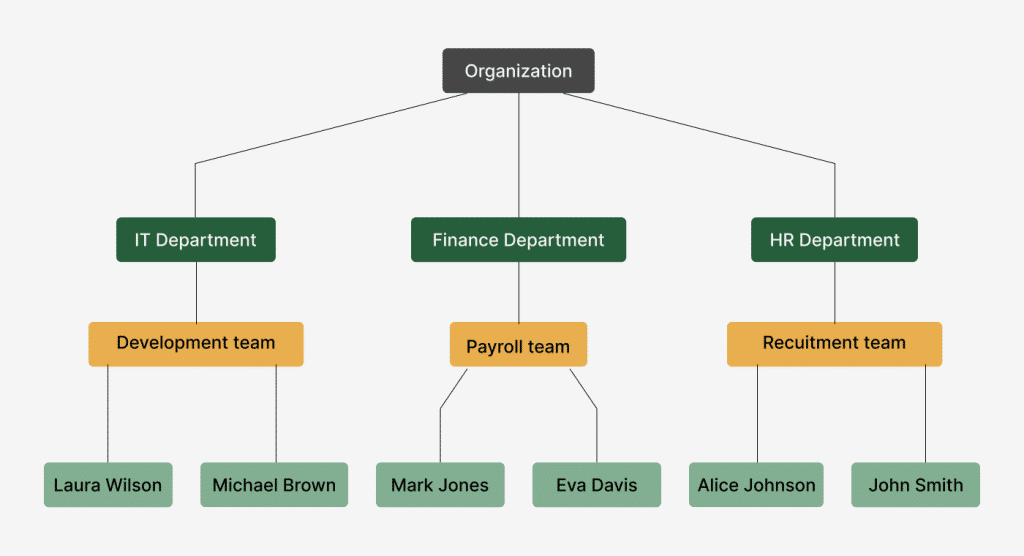
Now, let’s look at some methods for database design for storing tree in SQL, using a simple structure of an organization in the picture above.
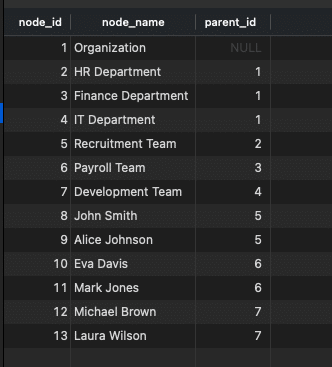
Adjacency List
Each node records its parent node.
Sample queries
(Below are some sample queries, the rest is in the attachments)
Select Full tree
WITH RECURSIVE FullTree AS (
SELECT node_id, node_name, parent_id, 1 AS level
FROM AdjacencyListHierarchy
WHERE parent_id IS NULL -- Assuming NULL represents the root node
UNION ALL
SELECT a.node_id, a.node_name, a.parent_id, ft.level + 1
FROM AdjacencyListHierarchy AS a
INNER JOIN FullTree AS ft ON a.parent_id = ft.node_id
)
SELECT node_id, node_name, parent_id, level
FROM FullTree
ORDER BY node_id;
Select Subtree
WITH RECURSIVE SubTree AS (
SELECT node_id, node_name, parent_id, 0 AS level
FROM AdjacencyListHierarchy
WHERE node_name = 'HR Department' -- Replace with the node you want to start the subtree from
UNION ALL
SELECT a.node_id, a.node_name, a.parent_id, st.level + 1
FROM AdjacencyListHierarchy AS a
INNER JOIN SubTree AS st ON a.parent_id = st.node_id
)
SELECT node_id, node_name, parent_id, level
FROM SubTree
ORDER BY node_id;
Select full path of a node
WITH RECURSIVE NodePath AS (
SELECT node_id, node_name, parent_id
FROM AdjacencyListHierarchy
WHERE node_name = 'Eva Davis' -- Replace with the node you want to find the path for
UNION ALL
SELECT alh.node_id, alh.node_name, alh.parent_id
FROM AdjacencyListHierarchy AS alh
INNER JOIN NodePath AS np ON alh.node_id = np.parent_id
)
SELECT GROUP_CONCAT(node_name ORDER BY node_id DESC SEPARATOR ' / ') AS full_path
FROM NodePath;
Summary
Advantages
- Easy to understand: It is the natural way we think about hierarchical structures.
- Easy to insert / delete: we only need to modify “parent_id” of a node.
- Flexible: it can represent many types of hierarchical structures, with varying levels of depth
Disadvantages
- Slow queries: since it requires recursive SQL queries, the performance will not be great.
- Complex query when retrieving full path of a node, especially when using recursive queries.
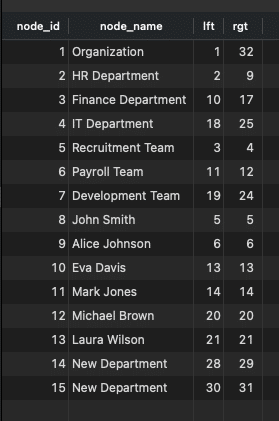
Nested set
We are using additional column, “lft” and “rgt” to store information about node’s position within the hierarchy. The child range will be inside the parent range. For example, in the image below, the “HR Department” is the child of the Organization because the range (2,9) is inside (1,32).
Sample queries
(Below are some sample queries, the rest is in the attachments)
Insert
-- Specify the name of the new node and the parent node where it should be inserted
SET @newNodeName = 'New Department';
SET @parentNodeID = 1; -- ID of the parent node ('Organization' in this case)
-- Calculate the rightmost right (rgt) value in the parent's subtree
SELECT rgt INTO @rightmostRgt
FROM NestedSetTree
WHERE node_id = @parentNodeID;
-- Increase rgt values of nodes greater than or equal to the rightmostRgt within the parent's subtree
UPDATE NestedSetTree
SET rgt = rgt + 2
WHERE rgt >= @rightmostRgt;
-- Increase lft values of nodes greater than or equal to the rightmostRgt within the parent's subtree
UPDATE NestedSetTree
SET lft = lft + 2
WHERE lft >= @rightmostRgt;
-- Insert the new node with calculated left and right values
INSERT INTO NestedSetTree (node_id, node_name, lft, rgt)
VALUES (
(SELECT MAX(node_id) + 1 FROM NestedSetTree), -- Calculate a new unique node_id
@newNodeName,
@rightmostRgt, -- New node's lft value
@rightmostRgt + 1 -- New node's rgt value
);
Select
SELECT node_id, node_name, lft, rgt
FROM NestedSetTree
WHERE lft >= 2 AND rgt <= 9; -- Replace with the appropriate lft and rgt values
ORDER BY lft;
Update a node
-- Specify the node_id of the node you want to move and the new parent's node_id
SET @nodeToMove = 8; -- Replace with the node_id you want to move
SET @newParent = 3; -- Replace with the node_id of the new parent
-- Find the left and right values of the node to move
SELECT lft, rgt INTO @nodeLft, @nodeRgt
FROM NestedSetTree
WHERE node_id = @nodeToMove;
-- Calculate the width of the node's subtree
SET @subtreeWidth = @nodeRgt - @nodeLft + 1;
-- Find the left and right values of the new parent
SELECT lft INTO @newParentLft
FROM NestedSetTree
WHERE node_id = @newParent;
-- Update the left and right values of nodes within the node's subtree
UPDATE NestedSetTree
SET
lft = CASE
WHEN lft BETWEEN @nodeLft AND @nodeRgt THEN lft + @subtreeWidth
ELSE lft
END,
rgt = CASE
WHEN rgt BETWEEN @nodeLft AND @nodeRgt THEN rgt + @subtreeWidth
ELSE rgt
END
WHERE
lft >= @nodeLft AND rgt <= @nodeRgt;
-- Update the left and right values of the node to move
UPDATE NestedSetTree
SET
lft = @newParentLft + 1,
rgt = @newParentLft + 2
WHERE
node_id = @nodeToMove;
Delete a node
-- Specify the node_id of the node you want to delete
SET @nodeToDelete = 2; -- Replace with the node_id you want to delete
-- Find the left and right values of the node to delete
SELECT lft, rgt INTO @nodeLft, @nodeRgt
FROM NestedSetTree
WHERE node_id = @nodeToDelete;
-- Calculate the width of the node's subtree
SET @subtreeWidth = @nodeRgt - @nodeLft + 1;
-- Delete the node and its subtree
DELETE FROM NestedSetTree
WHERE lft BETWEEN @nodeLft AND @nodeRgt;
-- Update the left and right values of remaining nodes
UPDATE NestedSetTree
SET
lft = CASE
WHEN lft > @nodeRgt THEN lft - @subtreeWidth
ELSE lft
END,
rgt = CASE
WHEN rgt > @nodeRgt THEN rgt - @subtreeWidth
ELSE rgt
END
WHERE
rgt > @nodeRgt;
Summary
Advantages
- Faster when finding ancestors, descendants, and subtrees because it does not require recursion.
- Stable performance: the performance is not affected by the tree’s depth.
Disadvantages
- Complex updates: inserting, updating or deleting nodes can be complex and requires careful management to maintain the integrity of the tree.
- Performance for inserts and updates: it is slow because it may require updating many rows, especially in deep hierarchies.
- Storage problem: it has additional column (lft, rgt) to maintain tree structure.
- Not suitable for frequent structure changes: because update tree structure is complicated, Nested set is not the best choice if your tree changes frequently.
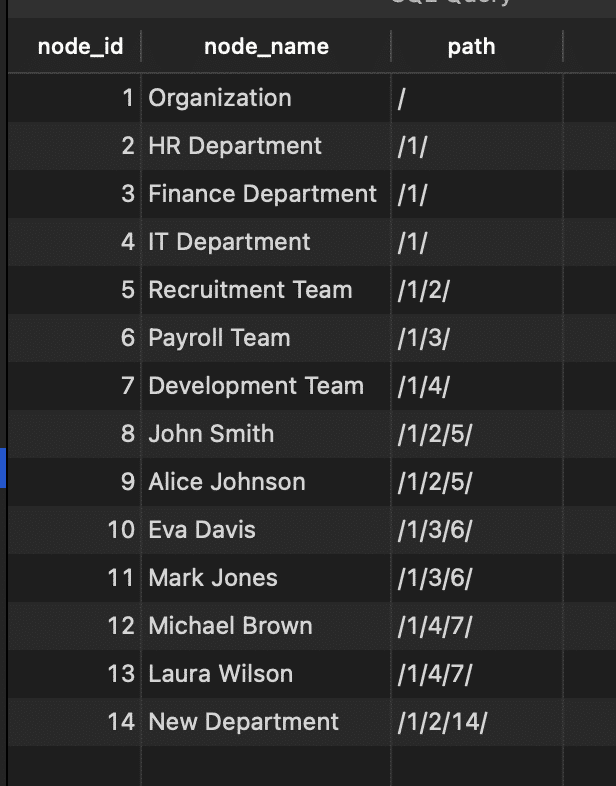
Path enumeration
This structure stores the path of each node related to other nodes inside of it. You can see it in the image below
Sample queries
(Below are some sample queries, the rest is in the attachments)
Select a tree
SET @parentPath = '/1'; -- Replace with the path of the parent node
-- Retrieve the subtree under the specified parent node
SELECT node_id, node_name, path
FROM PathEnumerationTree
WHERE path LIKE CONCAT(@parentPath, '%')
ORDER BY path;
Insert a node
-- Define the values for the new node
SET @newNodeId = 14; -- Replace with the desired node_id for the new node
SET @newNodeName = 'New Department'; -- Replace with the desired name for the new node
SET @parentNodePath = '/1/2/'; -- Replace with the path of the parent node
-- Generate the path for the new node
SET @newNodePath = CONCAT(@parentNodePath, @newNodeId, '/');
-- Insert the new node into the PathEnumerationTree table
INSERT INTO PathEnumerationTree (node_id, node_name, path)
VALUES (@newNodeId, @newNodeName, @newNodePath);
Change the path of a node
-- Specify the node_id of the node you want to move
SET @nodeIdToMove = 8; -- Replace with the node_id you want to move
-- Specify the new parent node's path
SET @newParentNodePath = '/1/3/'; -- Replace with the path of the new parent node
-- Retrieve the current node's path
SELECT path INTO @currentNodePath
FROM PathEnumerationTree
WHERE node_id = @nodeIdToMove;
-- Calculate the new path for the node
SET @newNodePath = CONCAT(@newParentNodePath, @nodeIdToMove, '/');
-- Update the node's path
UPDATE PathEnumerationTree
SET path = REPLACE(path, @currentNodePath, @newNodePath)
WHERE path LIKE CONCAT(@currentNodePath, '%');
Delete a node
-- Specify the node_id of the node you want to delete
SET @nodeIdToDelete = 8; -- Replace with the node_id you want to delete
-- Retrieve the path of the node to be deleted
SELECT path INTO @nodePathToDelete
FROM PathEnumerationTree
WHERE node_id = @nodeIdToDelete;
-- Delete the node and its descendants from the hierarchy
DELETE FROM PathEnumerationTree
WHERE path LIKE CONCAT(@nodePathToDelete, '%');
Summary
Advantages
- Simple: it is simple enough for developers to understand and implement.
- Easy to query: it is easy to query and retrieve the nodes, their descendants, their ancestors.
- Flexible: It can adapt many hierarchical structures, and does not require complex table schema.
Disadvantages
- Difficult to update: adding, updating or deleting nodes can be complex. It will need string manipulation and recursive operation to maintain the path.
- Ordering problem: it may require additional logic to sort the nodes.
Closure table
This method uses an additional table to store all relationships between nodes in the tree.

Sample queries
(Below are some sample queries, the rest is in the attachments)
Select a tree
-- Select all descendants of 'HR Department' and their distances
SELECT
CN.node_id AS descendant_id,
CN.node_name AS descendant_name,
CT.distance
FROM
ClosureNodes AS CN
JOIN
ClosureTable AS CT
ON
CN.node_id = CT.descendant_id
WHERE
CT.ancestor_id = 2; -- Node ID for 'HR Department'
Moving a node
-- // moving a node
-- Specify the node_id of the node you want to move
SET @nodeIdToMove = 8; -- Replace with the node_id you want to move
-- Specify the node_id of the new parent node
SET @newParentNodeId = 3; -- Replace with the node_id of the new parent node
-- Retrieve the closure relationships for the node to be moved
WITH MovedNodeClosure AS (
SELECT
CT.ancestor_id AS original_ancestor,
CT.descendant_id AS node_to_move,
CT.distance
FROM
ClosureTable AS CT
WHERE
CT.descendant_id = @nodeIdToMove
)
-- Update closure relationships for the moved node
UPDATE ClosureTable AS CT
SET
CT.ancestor_id = @newParentNodeId,
CT.distance = MovedNodeClosure.distance + 1
FROM MovedNodeClosure
WHERE
CT.descendant_id = @nodeIdToMove;
-- Update the moved node's closure relationships for descendants
UPDATE ClosureTable AS CT
SET
CT.ancestor_id = @nodeIdToMove,
CT.distance = CT.distance - MovedNodeClosure.distance - 1
FROM MovedNodeClosure
WHERE
CT.ancestor_id = MovedNodeClosure.original_ancestor;
-- Finally, update the moved node's parent_id in the main table
UPDATE ClosureNodes
SET
node_id = @nodeIdToMove,
node_name = (SELECT node_name FROM ClosureNodes WHERE node_id = @nodeIdToMove)
WHERE
node_id = @nodeIdToMove;
Delete a node
-- // delete a node
-- Specify the node_id of the node you want to delete
SET @nodeIdToDelete = 8; -- Replace with the node_id you want to delete
-- Retrieve the closure relationships for the node to be deleted
WITH DeletedNodeClosure AS (
SELECT
CT.ancestor_id AS deleted_ancestor,
CT.descendant_id AS node_to_delete,
CT.distance
FROM
ClosureTable AS CT
WHERE
CT.descendant_id = @nodeIdToDelete
)
-- Delete the closure relationships for the node and its descendants
DELETE FROM ClosureTable
WHERE
descendant_id IN (SELECT node_to_delete FROM DeletedNodeClosure);
-- Update the closure relationships for descendants of the deleted node
UPDATE ClosureTable AS CT
SET
CT.ancestor_id = DeletedNodeClosure.deleted_ancestor,
CT.distance = CT.distance - DeletedNodeClosure.distance - 1
FROM DeletedNodeClosure
WHERE
CT.ancestor_id = @nodeIdToDelete;
-- Delete the node from the main table
DELETE FROM ClosureNodes
WHERE
node_id = @nodeIdToDelete;
Summary
Advantages
- Simple to get data: it is easy to get information about ancestors, descendants, and path with simple join.
- Good reading performance: because it is precomputed data, it is very fast to query.
- Data integrity: it stores relationship between nodes, preventing inconsistent data.
- Support deep hierarchies: you can create unlimited depth tree with this structure without affecting the performance.
Disadvantages
- Complex updates: updating a node in closure table is very complex. When adding, moving or deleting nodes, it may require the recalculation of closure relationships.
- Storage problem: it uses extra tables to store relationship, so it will take more storage space.
- Maintenance issue: rebuilding the closure table or ensuring data integrity after updates can be complex and time-consuming.
- Not human friendly: it is not human-readable, so it is difficult to get the data directly.
Solution comparison
| Recursive query | Query performance | CUD complexity | More storage | |
| Adjacency list | yes | low | easy | no |
| Nested set | no | high | normal | yes |
| Path enumeration | no | high | normal | yes |
| Closure table | no | normal | hard | yes |
This is a short summary of each tree structure mentioned in the blog post. Each structure has its tradeoffs, so you must be the person who decides what structure will be used in your project, based on its advantages and disadvantages. If you have any questions about tree structures in SQL, feel free to reach out to zen8labs.
Happy coding!
Chien Nguyen, Software Engineer


